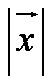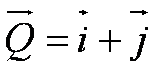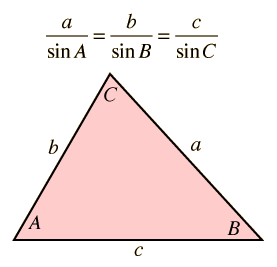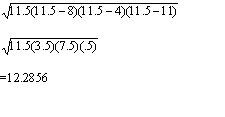First, I've posted the solutions to today's vector handouts on our
class website. The file is Vector Exercise Solutions.pdf
Here’s a list of topics for Friday’s test:
Precalculus Chapter 6 Test Topics:
Law of Sines given a triangle and directions (use a particular angle/side)
Law of Cosines given a triangle and directions (use a particular angle/side)
Area formulas given a triangle and directions (use a particular angle/side)
Uses of the Law of Sines and the Law of Cosines
Impossible Triangles
Ambiguous Triangles – visual
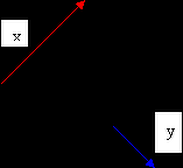
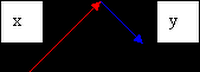
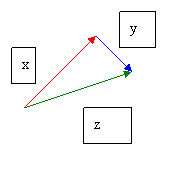
Sketch a resultant vector given two vectors
Determine horizontal and vertical components (i and j components)
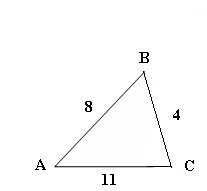
Solve triangles – missing sides, angles, areas
Add vectors – bearing and wind speed
Golf shot problems
That’s it! The format is as expected – ½ calculator, ½ non-calculator. I’ll be in my classroom on Thursday after school and before school on Friday. I’ll also be available online later on Thursday evening. If you have specific questions Thursday night, email me! And don't forget your holiday math songs are due on Monday...
See you in class!
In the spirit of the holidays:
Yes, Virginia, There is a Santa Claus
By Francis P. Church, first published in The New York Sun in 1897. [See The People’s Almanac, pp. 1358–9.]
We take pleasure in answering thus prominently the communication below, expressing at the same time our great gratification that its faithful author is numbered among the friends of The Sun:
Dear Editor—
I am 8 years old. Some of my little friends say there is no Santa Claus. Papa says, “If you see it in The Sun, it’s so.” Please tell me the truth, is there a Santa Claus?
Virginia O’Hanlon
Virginia, your little friends are wrong. They have been affected by the skepticism of a skeptical age. They do not believe except they see. They think that nothing can be which is not comprehensible by their little minds. All minds, Virginia, whether they be men’s or children’s, are little. In this great universe of ours, man is a mere insect, an ant, in his intellect as compared with the boundless world about him, as measured by the intelligence capable of grasping the whole of truth and knowledge.
Yes, Virginia, there is a Santa Claus. He exists as certainly as love and generosity and devotion exist, and you know that they abound and give to your life its highest beauty and joy. Alas! how dreary would be the world if there were no Santa Claus! It would be as dreary as if there were no Virginias. There would be no childlike faith then, no poetry, no romance to make tolerable this existence. We should have no enjoyment, except in sense and sight. The external light with which childhood fills the world would be extinguished.
Not believe in Santa Claus! You might as well not believe in fairies. You might get your papa to hire men to watch in all the chimneys on Christmas eve to catch Santa Claus, but even if you did not see Santa Claus coming down, what would that prove? Nobody sees Santa Claus, but that is no sign that there is no Santa Claus. The most real things in the world are those that neither children nor men can see. Did you ever see fairies dancing on the lawn? Of course not, but that’s no proof that they are not there. Nobody can conceive or imagine all the wonders there are unseen and unseeable in the world.
You tear apart the baby’s rattle and see what makes the noise inside, but there is a veil covering the unseen world which not the strongest man, nor even the united strength of all the strongest men that ever lived could tear apart. Only faith, poetry, love, romance, can push aside that curtain and view and picture the supernal beauty and glory beyond. Is it all real? Ah, Virginia, in all this world there is nothing else real and abiding.
No Santa Claus! Thank God! he lives and lives forever. A thousand years from now, Virginia, nay 10 times 10,000 years from now, he will continue to make glad the heart of childhood.
About the Exchange
Francis P. Church’s editorial, “Yes Virginia, There is a Santa Claus” was an immediate sensation, and went on to became one of the most famous editorials ever written. It first appeared in the The New York Sun in 1897, almost a hundred years ago, and was reprinted annually until 1949 when the paper went out of business.
Thirty-six years after her letter was printed, Virginia O’Hanlon recalled the events that prompted her letter:
“Quite naturally I believed in Santa Claus, for he had never disappointed me. But when less fortunate little boys and girls said there wasn’t any Santa Claus, I was filled with doubts. I asked my father, and he was a little evasive on the subject.
“It was a habit in our family that whenever any doubts came up as to how to pronounce a word or some question of historical fact was in doubt, we wrote to the Question and Answer column in The Sun. Father would always say, ‘If you see it in the The Sun, it’s so,’ and that settled the matter.
“ ‘Well, I’m just going to write The Sun and find out the real truth,’ I said to father.
“He said, ‘Go ahead, Virginia. I’m sure The Sun will give you the right answer, as it always does.’ ”
And so Virginia sat down and wrote her parents’ favorite newspaper.
Her letter found its way into the hands of a veteran editor, Francis P. Church. Son of a Baptist minister, Church had covered the Civil War for The New York Times and had worked on the The New York Sun for 20 years, more recently as an anonymous editorial writer. Church, a sardonic man, had for his personal motto, “Endeavour to clear your mind of cant.” When controversal subjects had to be tackled on the editorial page, especially those dealing with theology, the assignments were usually given to Church.
Now, he had in his hands a little girl’s letter on a most controversial matter, and he was burdened with the responsibility of answering it.
“Is there a Santa Claus?” the childish scrawl in the letter asked. At once, Church knew that there was no avoiding the question. He must answer, and he must answer truthfully. And so he turned to his desk, and he began his reply which was to become one of the most memorable editorials in newspaper history.
Church married shortly after the editorial appeared. He died in April, 1906, leaving no children.
Virginia O’Hanlon went on to graduate from Hunter College with a Bachelor of Arts degree at age 21. The following year she received her Master’s from Columbia, and in 1912 she began teaching in the New York City school system, later becoming a principal. After 47 years, she retired as an educator. Throughout her life she received a steady stream of mail about her Santa Claus letter, and to each reply she attached an attractive printed copy of the Church editorial. Virginia O’Hanlon Douglas died on May 13, 1971, at the age of 81, in a nursing home in Valatie, N.Y.