6.6 Vector Addition

6.6 Vector Addition

Vector: A line with a direction and a magnitude
-usually described as an arrow

"Vector x" can be described as an x with a line over it

If you only want to refer to the magnitude, put the absolute value bars around the symbol.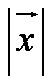

Resultant-found by adding the two vectors together
-to add them together, place them head to tail, so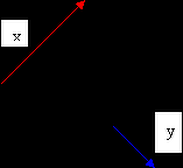


Would Become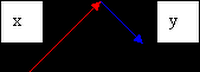

-create a third line, line z, to make a triangle.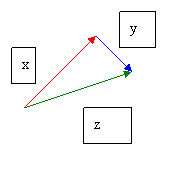



Once you have a triangle formed, use the law of sines/cosines to find side z. Side z is the resultant.


Another way you can find the resultant is by using a right triangle. This works if you are given two vectors and a direction angle.

Once you have moved the vectors head to tail, use the component formula to find the resulant motion.

Component Form: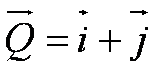

or
Q = A cosx i + A sinx j
Where Q is a vector where
A=Magnitude
x=Degree of Direction Angle


In other words, the component form is the
Length x cosA (for the x value) + Length x sinA (for the y value)

Note: If a problem ever talks about a bearing, the degrees will move clockwise from the direct north position.

Sample Problem

Shelly is walking in the park at a bearing of 90 degrees. After walking 200 yards, she turns to walk another 65 yards at a bearing of 42 degreed. How far is Shelly from her original point?

Set up a diagram with the resultant vector.

Convert the two given vectors to component for. One vector is 200yd at 90 degrees, and the other is 65yd at 43 degrees. Set up the two vectors' equations to look like

200Cos(90) + 200Sin(90)

and

65Cos(43) +65Sin(43).

Once you have converted the equations, add the two together.

[200Cos(90) + 200Sin(90)]i + [65Cos(43) + 65in(43)]

Answer: 291.868yds

Here's a website for additional help.
http://www.1728.com/vectutor.htm

Once again, I'm going to personalize with something bass related. I found this guy on YouTube who built an upright bass out of a cardboard box and a piece of plywood. It actually sounds really good!

http://www.youtube.com/watch?v=c6cTbaBApM4

Huzzah! It's Allison's Turn!