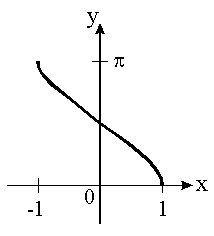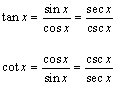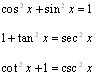Friday's Test Topics

Here’s a list of topics for Friday’s test:

Precalculus Chapter 5 Test Topics:
Composite Argument Properties (memorize! – sine and cosine)
Double Argument Properties (sine and cosine)
Understanding the implications of the +/- in the half-argument properties
Composition of Ordinates – sketch the graph of the sum or product of two given functions
Discussion/Illustration of co-function and odd/even properties
Numeric proof/demonstration of Composite Argument properties
Transform an equation given in terms of cosine with a phase displacement to a linear combination of sine and cosine
Transform an equation given as a linear combination of sine and cosine to an equation in terms of cosine with a phase displacement
Use a composite argument property to prove a co-function property
Use given values to compute composite functions
Compare algebraic computed values to calculator values
Harmonic analysis
Terminology
Composite Argument Identity
Application of Sum and Product Properties
Application of ½ -angle Properties

That’s it! The format is as expected – ½ calculator, ½ non-calculator. The calculator portion is significantly longer than the non-calculator portion, so budget your time accordingly. I’ll be in my classroom on Thursday after school and before school on Friday. I’ll also be available online later on Thursday evening. If you have specific questions Thursday night, email me!

See you in class!

"The best way to predict your future is to create it."
- Peter Drucker

Our Online Textbook

Ok, as promised, here's the link and class pass to our online textbook:

The website: http://www.keypress.com/PreCalc

Our class pass: 2901-a2e9cc0b7

Have fun studying!

Prep Precalculus D 2006-07

By the way, Annie you're next.

Prep Precalculus D 2006-07

Chapter 5 Section 6: Double and Half Argument Properties

So it's almost Christmas and what's a better gift than the Double and Half Argument Properties? I can't think of one. Enjoy! In this section we take a step beyond the composite argument property. When you write cos2x as cos(x + x) the composite argument property is used. A double argument property can result by expressing cos2x in terms of sines and cosines of x. Half argument properties can also be derived from the double argument properties.

PRODUCTS and SQUARES of COSINE and SINE
sin x cos x = 1/2 sin2x - Product of sine and cosine property
cos²x = 1/2 cos2x - Square of cosine property
sin²x=1/2-1/2 cos 2x - Square of sine property.

Example 1:
sin30 cos30 = 1/2 sin60 => 1/2 (root(3)/2) => root(3)/4
sin30 cos30 => 1/2 (root(3)/2) => root(3)/4

DOUBLE ARGUMENT PROPERTIES
This is how the double argument property for cosine is derived.
cos2x = cos(x + x)
= cos x cos x - sin x sin x
= cos²x - sin²x
- Double Argument for Sine: MEMORIZE
sin2A = 2sinA cosA
- Double Argument for Cosine: MEMORIZE
cos2A = cos²A - sin²A
cos2A = 2 cos²A -1
cos2A = 1 - 2 sin²A
- Double Argument Property for Tangent
tan2A = (2 tanA) ÷ (1 - tan²A)

HALF ARGUMENT PROPERTIES
- Half Argument Property for Sine
sin(1/2)A = +/- root(1/2(1-cosA))
-Half Argument Property for Cosine
cos(1/2)A = +/- root(1/2(1+cosA))
-Half Argument Property for Tangent
tan(1/2)A = +/- root((1-cosA)÷(1+cosA)) = (1 - cosA)÷(sinA) = (sinA) ÷ (1 + cos A)

Example 2:
Express the sin100 in terms of cos200.
First look for a connection between the two numbers.
100 is half of 200, so the Half Properties will be used.
Determine what quadrant the first term (sin100) falls into. It falls into quadrant II in this case, and the +/- before the square root becomes positive, since sin is positive in quadrant II. Finally plug the numbers into the equation.
sin100 = + root((1/2)(1-cos200))

Here are some additional links:
http://www.andrews.edu/~calkins/math/webtexts/numb18.htm

http://www.keymath.com/x7111.xml

So I could'nt get the picture I wanted into the blog, so here's a good quote. Two men were walking down the streets of New York. One was a busy businessman. The other man said to the businessman, "Wow, the crickets sound beautiful today." The businessman replied, "How can you possibly hear the crickets with all the noise around? All the taxis and people block out anything else." The first man responded, "You hear what you listen for."

5-5: The Sum and Product Properties

Ok, so today we worked on being able to change a certain phrase into another way of expressing it. For example:

If we were given the phrase cos12x + cos10x, we could change it into 2cos11xcosx. This is how we would do it:

cos12x + cos10x =
cos(11x + x) + cos(11x - x)= (for this step, you need to find two numbers that will add up to be the larger number in the original phrase and the difference will make the smaller number in the original phrase. You can find these numbers easily by using A-B/2 and A+B/2.) but now onto the next step!
cos11xcosx- sin11xsinx + cos11xcosx + sin11xsinx (the sines cancel out and you are left with 2cos11xcosx

In class we were given several formulas so we can transfer these phrases into other equal phrases. Here they are:
2cosAcosB = cos(A+B) + cos(A-B)
-2sinAsinB = cos(A+B) - cos(A-B)
2sinAcosB = sin(A+B) + sin(A-B)
2cosAsinB = sin(A+B) - sin(A-B)

sinx + siny = 2sin.5(x+y)cos.5(x-y)
sinx - siny = 2cos.5(x+y)sin.5(x-y)
cosx + cosy = 2cos.5(x+y)cos.5(x-y)
cosx - cosy = -2sin.5(x+y)sin.5(x-y)

Here is an example problem!
Given 2sin41cos24, transform this phrase into a sum.
2sin41cos24 --> 2sinAcosB = sin(A+B) + sin(A-B)
sin(41+24) + sin(41-24) = sin65 + sin17

If you are given a problem like sin2x + sin10x which takes you to the answer
2sin6xcos(-4x), you can make the (-4x) positive! If you remember that the cosine is an even function (meaning f(x) = f(-x)), then really -4x is the same as 4x. So you can just switch out the -4x for the 4x.

If you find yourself in the same problem with a sine function with the negative, remember that sine is an odd function meaning that sin(x) = -sin(x). So:
2sin13cos48 = sin61 + sin(-35) you can just change the sin61 + sin(-35) to sin61-sin35.

If you need more help on this section, check out this site:http://www.keymath.com/x7111.xml
Go to section 5.5 and click on the other links. The links are a little fancy looking, but they have the information on there.

Ok, I think Nick is next... Alright this is what we'll do. We'll keep going with the order like it is (nick, etc.) and when we come to Tara, she won't have to do it! THANKS TARA!

Here is my personal touch!
Once upon a time, there were three princes who wished to marry a princess. The princess wished to marry one of them, but not the other two. Her father however, was rather conservative, and did not feel she was ready to marry any of them. The King decided to put all three of them to tests that he believed none of them would be able to pass. First, he blindfolded them all, then led each in turn to his individual test.
The King led Prince #1 to the base of a mountain where there were ten painted, wooden doors, glistening in the sun. "All but one of these doors in front of you are white," said the King. "If you can tell me within the next ten minutes, which door is black, then you may marry my daughter. You may not speak to anyone, and you may not remove your blindfold."
The King led Prince #2 to a hillside, and pointed out across his lush green valleys to the edge of his kingdom, where ten beautiful buildings stood. "All but one of these buildings in front of you are white," the King said. "If you can tell me within the next ten minutes, which building is black, then you may marry my daughter. You may not speak to anyone, and you may not remove your blindfold."
The King led Prince #3 to a magnificent dining table where ten places were impeccably laid out. "All but one of the napkins on this table are white," said the King. "If you can tell me within the next ten minutes, which napkin is black, then you may marry my daughter. You may not speak to anyone, and you may not remove your blindfold."
Ten minutes later, only one of the princes - the one the princess wished to marry - had succeeded at his individual test. Which one of the princes had succeeded?

Want the Answer? Here it is:
Prince #1 succeeded at his test.
How did the prince solve the test? He felt each of the doors in turn. As it was a sunny day, the black one was much hotter to the touch than the white ones, which absorbed less heat.

YAY FOR SECTION 5-5!!!

5.4 Composition of Ordinates and Harmonic Analysis

Hey guys! Welcome back from Thanksgiving break-what better way to start off the week than with a lesson on combining sinusoidal graphs with different periods?!

Let's start with breaking down the title...
Composition of ordinates: Adding or multiplying sinusoids
Harmonic analysis: Finding the parent sinusoids from the new sinusoid

COMPOSITION OF ORDINATES

Some general tips to remember when drawing the new graph:
1. The points that make up the new graph are found by either adding or multiplying the corresponding ordinates of the parent graphs, meaning that for each x or theta value that we choose, we must find the y-value. (We can also look at this as adding or multiplying amplitudes)

2. Look for points that are easily identifiable.

3. Focus on the zeros, maximums, and minimums of the smaller graph; work off of the big graph using these points.

Differentiating between the Sum of Two Sinusoids and the Product of Two Sinusoids:
Sum: There is no constant sinusoidal axis, but the larger parent graph becomes the midpoint of the new graph (inner curve).

In this graph, the parent curves are in red and blue and the resulting curve is in green, representing the sum of the two parent sinusoids.

Product: There is a constant sinusoidal axis, and the larger parent graph becomes the boundary of the new graph (envelope curve).

In this graph, the parent curves are in red and blue and the resulting curve is in purple, representing the product of the two parent sinusoids.

HARMONIC ANALYSIS (EYE TO EYE WITH THE MONSTER)

The Procedure:

1. Determine whether or not it is Product or Sum based on whether or not it has a constant sinusoidal axis.
2. Draw the larger curve and determine its equation.

If it is a product...
3. Find the midpoint of the larger cycle and look for symmetry. If the graph is symmetrical around the midpoint, this means that both trigonometric functions are the same.
4. Count the contact points and then subtract 1, in order to get the number of cycles. Use this number as the coefficient of x or theta in the second half of the equation. (For example, this number would be placed where the 11 is: y=5sinxsin11x)
Hint: The 5 in this equation represents the dilation of both functions in the product; the amplitude of the shorter-cycle fucntion is always 1


If it is a sum...
3. Determine whether the sum is *sin + cos, cos + sin, sin + sin, cos + cos* by looking at the origin for symmetry.
4. Find the amplitude of the smaller curve by finding how far above and below the big curve it reaches. (This number will be placed where the 2 is: y=4costheta + 2sintheta)
5. Find the contact points the same way, subtracting 1 to get the number of cycles, and then before inserting this number as the coefficient of theta/x in the second part of the equation, multiply it by the coefficient of theta/x in the first part of the equation. (If we are finishing teh equation y=4cos45theta +2_____ and we have 10 cycles, the equation becomes y=4cos45theta + 2sin450theta)

Example Problem:
Harmonic Analysis: Find the particular equation for this graph.

1. Because we can see that this graph has a constant sinusoidal axis, we know that it is a Product.
2. Next we determine an equation for the larger curve, whose trigonometric function we know to be sin, because the graph goes through the origin. We also know that it has an amplitude of 6, so its equation is: 6sintheta
3. We can see that the graph is symmetrical at x=180, so we know that the second trigonometric function in our equation will be sin, the same as the first.
4. Now, we have to count the number of cycles, which we find by counting the contact points and then subtracting 1. There are 12 contact points, so there are thus 11 cycles. We insert this value into the second half of our equation: sin11theta
5. We are now ready to combine the two halves of the equation!! When we multiply our answer from #2 with our answer from #4, we get the equation: y=6sinthetasin11theta

For More Information:
If you'd like to get more information on this topic, check out this site: http://www.keymath.com/x7188.xml
It is actually a link off of a website that is all about our textbook; it offers extra information pertaining to the subjects we cover, so you could use it as a resource throughout the year. Hopefully the author included (Surprise?!) on the exciting website problems.

Nick...YOU'RE UP NEXT!! Just in case you guys are confused as to why we're going out of order, don't forget that I'm subbing for Natalie.

This is a picture of my sister and me with my cousin, Tamar. She's 10 years old, and she's an amazing gymnast. This picture was taken during the summer after my 9th grade year in her backyard in Cheyenne, Wyoming.

Harmonic Analysis Practice

Hi everyone! I know today's class was a lot to think about - I've uploaded some worksheets to the class website that have proven to be helpful in exploring the concepts. The file name is Precalc_EXP_05.pdf. If you're confused, these should help!

Serious-minded people have few ideas. People with ideas are never serious.
- Paul Valery

5-3 Composite Argument Properties

This section is all about lots of equations!!

The Odd-Even Properties
Even
cos (x) = cos (-x)
sec (x) = sec (-x)
Odd
sin(x) = -sin (-x)
csc(x) = -csc (-x)
tan (x) = -tan (-x)
cot (x) = -cot (-x)

The Cofunction Properties:
Degrees
cos theta = sin (90 degrees - theta)
sin theta = cos (90 degrees - theta)
cot theta = tan (90 degrees - theta)
tan theta = cot (90 degrees - theta)
csc theta = sec (90 degrees - theta)
sec theta = csc (90 degrees - theta)
Radians
cos x = sin (pi/2 - x)
sin x = cos (pi/2 - x)
cot x = tan (pi/2 - x)
tan x = cot (pi/2 - x)
csc x = sec (pi/2 - x)
sec x = csc (pi/2 - x)

The Composite Argument Properties for Cosine, Sine, and Tangent
Cosine
cos (A-B) = cosAcosB + sinAsinB
cos (A+B) = cosAcosB - sinAsinB
Sine
sin(A-B) = sinAcosB - cosAsinB
sin(A+B) = sinAcosB + cosAsinB
Tangent
tan (A-B) = (tanA - tanB) / (1 + tanAtanB)
tan (A+B) = (tanA + tanB) / (1 - tanAtanB)

You can use these properties to solve trigonometric equations algebraically.

Example Problem:

Find the general solution for x algebraically

cos xcos80 - sinxsin80 = 5

Since the composite argument property for cos(A+B) = cosAcosB - sinAsinB,

cos(x+80) = 0.5
x+80 = arccos 0.5
x = -80 arccos 0.5
x = -80 plus/minus inverse cos (0.5) + 2 pi n
x= 2 pi n - 80 plus/minus 1.047198...


For more help go to http://www.andrews.edu/~calkins/math/webtexts/numb18.htm#COFU
Natalie you're next!

Here's a puzzle that is usually attributed to Einstein, who may or may not have written it.

There are 5 houses in 5 different colours. In each house lives a person of a different nationality. The 5 owners each drink a certain type of beverage, smoke a certain brand of cigar, and keep a certain pet. Using the clues below can you determine who owns the fish?

The Brit lives in a red house.
The Swede keeps dogs as pets.
The Dane drinks tea.
The green house is on the immediate left of the white house.
The green house owner drinks coffee.
The person who smokes Pall Mall rears birds.
The owner of the yellow house smokes Dunhill.
The man living in the house right in the middle drinks milk.
The Norwegian lives in the first house.
The man who smokes Blend lives next door to the one who keeps cats.
The man who keeps horses lives next door to the man who smokes Dunhill.
The owner who smokes Blue Master drinks beer.
The German smokes Prince.
The Norwegian lives next to the blue house.
The man who smokes Blend has a neighbour who drinks water.





...supposedly according to Einstein 98% will not solve this.






The German owns the fish.

5-2 Composite Argument and Linear Combination Properties

Hey class. Today we learned about the Linear Combination Property. This property is used to find the amplitude and phase displacement when you combine cosine and sine equations(this is called a Linear Combination).

Linear Combination: b cos(x)+c sin(x)

Linear Combination Property:
b cos(x)+c sin(x) = A cos(x-D)
where
A = (b^2+c^2)^.5 (square root) and
D = arctan(c/b)

You determine the quadrant that the angle is in with A. If D is negative then add 180 degrees. This is because arctan= tan^-1(theta)+180n

We also learned about the Composite Argument Property for Cosine(A-B) which is used to solve cosine equations that have addition or subtration in them.

Composite Argument Property for Cosine (A-B):
cos(A-B) = cos(A)cos(B)+sin(A)sin(B)

Practice Problem
Find the Acos(x-D) equation for y=-8cos(theta)+3sin(theta)
A= square root of (-8^2+3^2) or square root (73)
D= tan^-1(3/-8) = -21 degrees
-21 degrees negative so add 180 degrees to D to get
D=159 degrees

Answer: square root of (73)*cos(theta-159)


For more on these concepts go to:
http://www.keymath.com/x7186.xml

Tight Poem by Sylvia Plath:
http://www.angelfire.com/tn/plath/daddy.html

Debbie I think that you are up next!

Chapter 4 Review Test Solutions

Just a quick note - I've posted a document with the solutions to the Chapter 4 practice test on our class website: http://courses.flintridgeprep.org/precalcDE/

See you tomorrow!

Wednesday's Test Topics

Here’s a list of topics for Wednesday’s test:

Precalculus Chapter 4 Test Topics:
Basic properties – Pythagorean, Reciprocal, Quotient
Equations versus Identities
Strategies and thought processes in solving Identities
Arcfunctions – graphical representations of arcsine, arccosine and arctangent
Arcfunctions versus inverse trig functions – criteria for selecting principal branches
Transformations and Identities
Determining solutions to trigonometric equations – graphically and algebraically
Domains and Ranges of Inverse Trigonometric Functions

That’s it! The format is as expected – ½ calculator, ½ Non-Calculator. I’ll be in my classroom on Tuesday after school, at the JPD rehearsal Tuesday evening and before school on Wednesday. I’ll also be available online later on Tuesday evening. If you have specific questions Tuesday night, email me!

See you in class!

The best years of your life are the ones in which you decide your problems are your own. You do not blame them on your mother, the ecology or the president. You realize that you control your own destiny.
-- Albert Ellis

4-6: Inverse Trigonometric Relation Graphs

Chapter 4 Section 6: Inverse Trigonometric Relation Graphs

Main Concepts:

Graphs and Principal Branches:

The Definition of arcsin, arctan, and arccos:
Using sine as an example, arcsin x means any of the angles whose sine is x. Arctan and arcos have the same meaning. The problem with this is that the entire graph will not be a function because it does not pass the vertical line test. Therefore, you must take the principal branch of the graph to make it a function. An inverse trigonometric function is a reflection of one branch of the graph across the line y=x. In choosing the principal branch, you must:
1. Include the entire domain
2. Include the origin, or make it as centrally located as possible
3. It must be a function
4. It should be a continuous graph
5. Choose the positive branch if possible

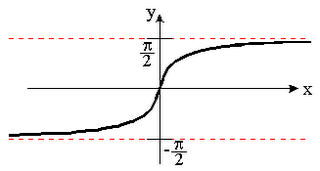
The Graph of Arcsin:The Graph of Arccos:The Graph of Arctan:

The principal branches of the graphs:

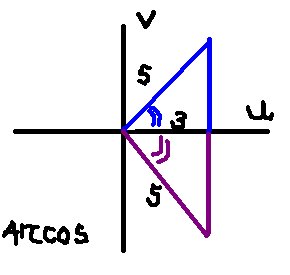
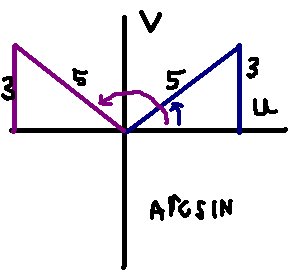
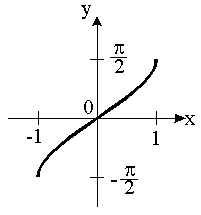• The Graph of Inverse Sine:Keep in mind that the domain of the original sine function becomes the range of its inverse. Domain: [-1, 1]; Range: [o, π]; In reference to the (u,v) coordinate system: Quadrants I and II

• The Graph of Inverse Cosine:

Domain: [-1, 1]

Range: [-π/2, π/2]

Quadrants I and IV

• The Graph of Inverse Tangent:

Domain: all real numbers

Range: [-π/2, π/2]

Quadrants I and IV

• For the other inverse trigonometric functions:

• Inverse cotangent:

Domain:[-1, 1]; Range: [0, π]; Quadrants I and II

• Inverse secant:

Domain:the absolute value of x ≥ 1; Range: [0, π] and y ≠ π/2; Quadrants I and II

• Inverse cosecant:

Domain:the absolute value of x ≥ 1; Range: [-π/2, π/2] and y ≠ 0; Quadrants I and IV

You can graph inverse trigonometric functions in parametric mode:

x1= sin (T)

y1= T

x2= cos (T)

y2= T

x3= tan (T)

y3= T

This will give you the entire graph of the inverse; even when it is not a function.

When you are in function mode and you graph these, your calculator will give you the graph of a function (like the restricted graphs shown above).

Exact Values of Inverse Circular Functions:

You can geometrically figure these types of problems out by creating a triangle from the given information.

Such as with cos(sin^/1(4/5))

• you can create a 3-4-5 triangle with this information and figure out the cosine of this angle is 3/5

• <--- The angle we are referring to.

• Sine= opp/hyp, so 4/5 and then you fill in the remaining side. Cosine= adj/hyp, so 3/5

• The Composite of a Function and Its Inverse Function:

f(f^-1(x)) = x and f^-1(f(x)) = x

This holds true only if the "x" is within the range of the outside function and the domain of the inner function.

Example Problem:

Using the concept that we learned about composite functions and their inverse functions:

Remember, f(f^-1(x)) = x and f^-1(f(x)) = x.

Problem:

cos(cos^-1(3/5)) = ?

3/5 is within the range of the outside function and the domain of the inside function, so the answer is 3/5.

For sin(sin^-1(4/5))

the answer is 4/5 because 4/5 is within the range of the outside function and the domain of the inside function.

For sin(sin^-1(5/3))

5/3 is not within the domain of the inside function. The domain of this function is [-1,1] and 5/3 is greater than one. Therefore, sin(sin^-1(5/3)) ≠ 5/3

Link for additional reference: http://www.sparknotes.com/math/precalc/trigonometricfunctions/section4.rhtml

This is my favorite painting...

****Reminder: Debby! You're up again! Good Luck!!!

Prep Precalculus D 2006-07

Lesson for chapter 4-4: Arcsine, Arctangent, Arccosine, and Trigonometric Equations
This section is

about...
1) solving for the theta or "x" (all the angles that have the same sin value, tan value or cos value)
2) memorizing the equations for arccos, arcsin and arctan
3) being able to visualize the reference triangles involved

Okay, so to review, we learned that to solve...
cos(x)=a
1st step) you have to use the arccos --> x= arccos(a)

2nd step) then simplify to what arccos actually means --> x= +/- inv. cos (a) + 2 pi(n)
What does it mean?
The arccos means that you solve for all the angles "x" that have a ratio "a" of adjacent/ hypotenuse in their reference triangles.
The reason we have the "+/-" (plus or minus) before the "inverse cos" is because... there are two angles on the "u, v coordinate system" that have the same ratio of adjacent leg/ hypotenuse.

For example: If the problem was, cos(x)=3/5... you can picture two reference triangles that yield this same ratio of adjacent side 3 and hypotenuse 5... It would look like this..

The blue reference triangle: adj 3 & hyp 5 (ratio of 3/5) and the purple ref triangle: adj 3 & hyp 5 (ratio of 3/5)
Blue angle= inv. cos (3/5)
purple angle= negative inv. cos (3/5)
Now add periods (2pi or 180 degrees) to both blue and purple angles to get the angles in all the other periods.
Equation for arccos:

x= +/-inv. cos (3/5) +2pi(n)
Note: the (3/5) is the number ratio of adj/hyp

Also note: REMEMBER to be in the right MODE, use radian mode for pi's and x's. Use degree mode for theta's and substitute 360 for 2pi.

Arcsine
arcsin (x) means all the angles whose sin is x (or all the angles that have the same ratio of opposite/hypotenuse) So, when you think about sin(x)=(3/5)...draw it out like this...

To get the angles whose sine is 3/5, you can draw 2 triangles... the blue reference triangle: opp side of 3 & hyp 5.
the purple ref triangle: opp side of 3 & hyp 5
This means that the blue arrow and the purple arrow represent 2 angles whose sin ratios = 3/5.
Blue angle= inv. sin (3/5)

purple angle= pi - inv.sin(3/5)
To get the purple angle you subtract the blue angle from pi (180degrees) because the ref angles are equal. Now add periods (2pi) to both the blue and purple angle to get the rest of the angles in all the other periods.
Equations for arcsin: x=inv.sin(3/5) +2pi(n)

or ... x= pi -minus inv.sin(3/5) + 2pi(n)

Arctan
Arctan(x) means all the angles whose tan is x.
So for the problem: tan(x)=3/5, think about all the angles whose opp = 3 and adj=5

First draw the reference triangles...

To get the angles whose tangent is 3/5, you can draw two triangles–
1)the blue ref triangle with an opp side 3 & adj side 5
2)the pink ref triangle with an opp side -3 & adj side -5 (this ratio of -3/-5 simplifies to 3/5)
blue angle= inv.tan (3/5)
to get to the pink angle you have to add pi(180 degrees)...
pink angle= pi + inv.tan(3/5)
to get to the blue angle again by going around the circle, you add pi.
Next blue angle= 2pi + inv.tan(3/5)
Therefore, you get to the next angle by adding pi, which is the period of the tan graph!
Equation for arctan: x= inv.tan (3/5) + pi(n)

note: (3/5) is the ratio for this specific problem

This makes sense when looking at the tangent graph because when you draw the line at y=3/5, there is only one intersection period of pi(180deg).
(sorry the pictures don't want to upload at all)

Whereas, in the sine (red) and cosine graph (blue) there are two intersections per period of 2pi(360deg), reflected in the two angles per period of 2pi for which the ratios are the same in the u, v coordinate plane.


Note: for all of these arc equations, you can solve for degrees by using 360degrees instead of2pi and 180degrees instead of pi. and again CHECK THE MODE
Interval Notation: another way to write the domain
A Closed interval
1)includes the end points
2) greater than or equal to / less than or equal to
3)is written with [brackets]
4)for example [0,4] means 0
An Open Interval
1)does not include the end points
2) > or <>

3) is written with (parentheses)

4) For example (o, pi) means 0

Note: You can combine the closed interval and open interval:
example: (0,2] ...this means x is greater than 0 and less than or equal to 2
New Symbol: *i can't insert the symbol...so it basically looks like a flattened capital e*

What does it mean? it means that x is in the domain of/ "in the element of"...
example: X *special symbol*[-400,3) ...means that x is greater than or equal to -400, and x is less than 3.


Practice Problem
Solve the equation 10 sin (x- .2) = -3 algebraically for x in the domain [0,4pi]. Show that your answers correct on a graph.

10 sin (x - .2) =-3

To solve for x, you can divide by 10 to isolate x on one side of the equation.
sin ( x-.2) = -.3 Take the arcsin of both sides to cancel the sin from the right side and further isolate the x.
(x- .2) = arcsin(-.3) Now, add the .2 to each side.
X = .2 + arcsin (-.3) Substitute the inv. sin equivalent for arcsin
x= .2 +sin (-.3) +2n or x=.2+ (-sin(-.3) +2n Simplify
x= -.105.. +2n or x= 3.646 +2n Now, find the solutions within the domain 0#x#4
x= 3.646, 6.178, 9.929, 12.462
To check your results, you can graph the original equation: y=10sin(x-.2) and what you set it equal to: y=-3 into your calculator graph. Now, find where they intersect in the given domain using the "calc" program.
Links for further information on inverse trig functions...

http://www.themathpage.com/aTrig/inverseTrig.htm
Celene!!! You are next to blog!
i really want to finger paint like this little girl. I would definitely choose it as my major in college.

Wednesday's Quiz Topics

Here’s a list of topics for Wednesday’s quiz:

Precalculus Quiz 4.1-4 Topics
Quotient Properties
Reciprocal Properties
Pythagorean Properties
Strategies for proving Identities
Identities/Transformation of expressions – Algebraic
Identities/Transformation of expressions – Graphic
Arcsine, Arccosine, Arctangent – sketch and general formula
Solving Arcsine, Arccosine, Arctangent algebraically


That’s it. I’ll be in early on Wednesday and available after school on Tuesday. See you in class!

An Old Cherokee describes an experience going on
inside himself....
"It is a terrible fight and it is between two wolves.
One is evil - he is anger, envy, sorrow, regret,
greed, arrogance, self-pity, guilt, resentment,
inferiority, lies, false pride, superiority, and ego.

The other is good - he is joy, peace, love, hope,
serenity, humility, kindness, benevolence, empathy,
generosity, truth, compassion, and faith. This same
fight is going on inside you - and inside every
other person, too."

The grandson thought about it for a minute and then
asked his grandfather, "Which wolf will win?"

The old Cherokee simply replied, "The one you feed."

4-3 Identities and Algebraic Transformations of Expressions

Hey, it's Ellen! Here's what we did on 11/1/06 (All Saints' Day!) for math:

Summary: This lesson's basically about using what we know about trigonometric functions (the relationships we learned yesterday) and using them to either prove identities or to make one equation look like another one. The basic concept behind it is simple, but it can get a little complex somtimes. So here we go...

There's basically seven steps in either transforming an equation or proving an ID (identity):

1. Start by writing out expressions.
2. Determine difference and similarities.
3. Choose a point of attack!!!
4. Sin and cos approach (this step usually makes solving an equation easier, but may be inefficient at some times)
5. Use algebra technics (such as finding a common denominator, multiplying, etc).
6. Look for trigonometric relationships (fractions usually mean its a quotient ID while something squared usually means its a Pythagorean ID).
7. Repeat until the goal is achieved (like shampooing your hair ;D ).

Now that you know basically what to do, here are some examples:

Easy example:

Make sinx cotx look like cosx.

First off, what are the similaries and differences?
There are no same terms on either side of the equation! So we have to figure out a way to get the same terms. Plan of attack: use the quotient ID for cot!
Now it looks like this:




A little more challenging example is:



Now sometimes, you'll be proving ID's. Here's an example of a simple problem where the Pythagorean ID of sinx is proved:



*Note: The book recommends that when solving these types of equations, it's wise to only focus on one side of the equation and solve only that portion until it looks like the other portion. however, Mr. French thinks it's okay to work with both sides of the equation as long as in the end the two are identical. He believes that it still shows that you understand the concept.

**IMPORTANT NOTE: NEVER move parts of an equation from one side to another. NEVER. This violates the point of proving an ID!


Here's a complex example of proving an ID:



Another really complex example is:



It was hard finding a website that deals with this subject directly. But here's one. Click Here

One last thing before I go, here's some pictures of my new baby cousin Andrew!! Isn't he soo adorable?!?!



*yawn*



haha what an interesting expression xD



:)




OH, I ALMOST forgot! LUCY you're up NEXT! G'luck!

Random Note: Did you know tomorrow's National Deviled Egg Day--November 2! lol weird...o.O

4-2 Pythagorean, Reciprocal, and Quotient Properties

Lesson 4.2

Hey guys so today we learned how to derive algerbraically three kinds of properties expressing relationships among trigonometric functions.

All of these properties make it possible to show how two unlike looking things actually are equal to each other.

Reciprocal Properties:

• Reciprocal properties are just one over cosecant, secant and cotangent to get sin, cos and tan respectively.
  

Quotient Properties:

Pythagorean Properties:

Pythagorean properties are all based off of the first equation listed here. (To find the second equation, we just divided by cos^2. To find the third equation, we just divided by sin^2.)

Example Problem:

Show algebraically how tan x can be transformed into sec x /csc x using the quotient properties.

tan x = sin x / cos x = [(1/ csc x) / (1/sec x)] = sec x / csc x

Extra Help:

For a list of the properties go to: http://www.gomath.com/htdocs/ToGoSheet/Trigonometric/properties.html

For extra explinations go to: http://library.thinkquest.org/20991/alg2/trig.html

Reminder: Ellen you are next!

Haha i want to meet this little girl: