6.2 Oblique Triangles: Law of Cosines

Is everyone excited for the law of cosines?? I know I am!!! Especially since it's all festive in Christmas colors!

Oblique Triangles: Law of Cosines

If you are given three triangles with given sides 3 and 4 and included angles of 60º, 90º, and 120º:
In a right triangle, you can find the third side by using the Pythagorean Theorem:
a squared + b squared = c squared

However, in the 60º triangle, the value of c is less than a + b . For the 120º triangle, the value of c is greater than a + b .

The equation you will use to find the value of the third side from measures of two sides and an included angle is the Law of Cosines (since it involves the cosine of an angle).

OBJECTIVES:

• Given two sides and the included angle of a triangle, use the law of cosines to find the third side
• Given three sides of a triangle, find the angle

PROPERTY: The Law of Cosines

In tirangle ABC with sides a, b, and c,

a squared = b squared + c squared - 2bc cos A

Notes:

• if the angle is 90 degrees, the law of cosines reduces to the Pythagorean Theorem, because cos 90 degrees is zero.
• if A is obtuse, cos A is negative. so you are subtracting a negative number from b squared + c squared, giving the larger value for a squared.

Applications of the Law of Cosines

you can use the Law of Cosines to calculate either a side or an angle. In each case, there are different parts of a triangle given.

EXAMPLE 1:

Find side b in triangle ABC, if a = 7 cm, c = 10 cm, and angle B = 71 degrees

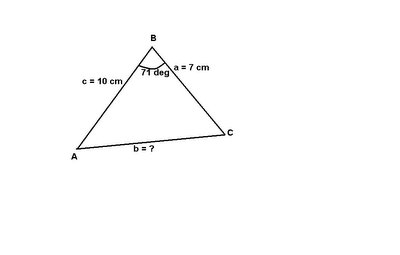
Solution:

b squared = 7 squared + 10 squared - 2(7)(10) cos 71 deg

b squared = 49 + 100 - (140 cos 71 deg)

b squared = 149 - (140 cos 71 deg)

b squared = 103. 4204...

*take the square root of both sides and then you get

b = 10.17 cm

EXAMPLE 2:

Find angle B if a = 7 ft, b = 14 ft, and c = 11 ft

Solution:

14 squared = 7 squared + 11 squared - 2(7)(11) cos B

196 = 49 + 121 - 154 cos B

196 = 170 - 154 cos B

*subtract 170 from 196

26 = - 154 cos B

*then divide -154 into 26

-13/77 = cos B

*then take the inverse cos of that fraction to get the value of angle B

cos -1 (-13/77) = B

Angle B = 99.72 deg

Want additonal help?

go here: http://mathworld.wolfram.com/LawofCosines.html

Personalization:

Becasue I was dressed so colorfully one day last week, that inspired my friend Taylor to draw me a super awesome picture:

Anna, you're up next!! (we got the best chapter ever. woot!)