Lesson 6-4, Law of Sines

Hey everyone
In class today, we learned the concept of Law of Sines.
Law of Sines



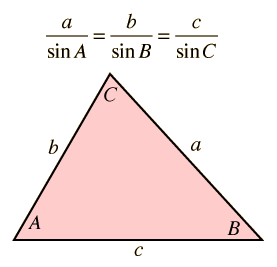
a/SinA= b/SinB= c/SinC

Verbally: With any triangle, the ratio of the sine of an angle to the length of the sides opposite that angle is constant.







Dealing with law of sines, some geometry terms should comeback.

Terminology= SAS= Side, Angle, Side
AAS=Angle,Angle,Side
SSS=Side,Side,Side
SSA=Side,Side,Angle
ASA=Angle,Side,Angle

Objective- We use our geometry terminology and law of sines to figure out all missing angles and sides. Always becareful is all the information is provided.

Law of Sines should only be used to come up with the leg of the triangle. You can use the law of sines to find an angle of a triangle, but one gets two values of the inverse sine relation between 0 and 180, either could be the answer. If one uses the law of cosine, one will achieve one answer to the angle.

Example #1


Angle B= 64 Angle C= 38 Side b= 9 ft
Figure out the missing info. Case= Angle, Angle, Side


Angle A= 180 -(38+64)
Angle A= 78



Sin 64/9= Sin38/c
Sin 64(c)= Sin 38(9)
c= Sin38(9)/Sin64
c=6.1648

Sin 64/9= Sin 78/a
(9) sin (78)= Sin(64)(a)
(9)Sin 38/ Sin 64=a
a=9.79

Example #2
In ABC triangle, A= 52 degrees, B= 31 degrees, a= 8 cm
Find side b and side c.

52+31=83
180-83
Angle C=97 degrees

Sin (97) /c=Sin(52)/8
Sin(52)c=Sin(97)8
c=Sin(97)8/Sin(52)
c=10.076

Sin(31)/b=Sin(52)/8
Sin(52)b=Sin(31)(8)
Sin(31)(8)/Sin(52)=b
b=5.228


Internet Source
http://home.alltel.net/okrebs/page93.html

Reminder

Claire you are up next have fun.

Personal Touch

I am a huge sports guy, I like basketball, football, soccer, tennis, and etc. So here is a picture of my favorite college and professional basketball teams.

Lakers UCLA