6-3 Area of a Triangle
Hey guys! So we officially only have wednesday, thursday, friday, another week after that and then four days after that till christmas break!!!! That's only 12 days- we can do it!...
Anyway lets learn about the Area of a Triangle...
Objective:
Given the measures of two sides and the included angle, find the area of the triangle.
Property: Area of a Triangle:
As we already know the area of a triangle = (1/2)(base)(height)
We can alter this formula to equal:
sin A= h/c
h= c sin A which can then be replaced in the original A= (1/2)(b)(h) to equal:
Area = (1/2)bc sin A
The area of a triangle equals half the product of two of its sides and the sine of the included angle.
Example Problem 1:
Find the area of triangle ABC given:
a=12 in.
b=10 in.
c= 62 degrees We can plug this into the formula Area = (1/2)bc sin A to get
A= (1/2)(10)(12) (sin62) = 52.9768 in. squared
Property: Hero's Formula: (Hero)
(Hero)
In triangle ABC, the area is given by
Area= ![]()
where s is the semiperimeter (half the perimeter) found by taking 1/2 (a+b+c)
Example Problem 2:
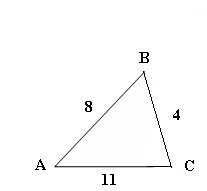
Use Hero's Formula to calculate the area of this triangle.
a= 4
b=11
c= 8
The perimeter (4+11+8) = 23 so s= (1/2)(23)= 11.5
A=
For Extra Help go to:
http://regentsprep.org/regents/mathb/5E1/areatriglesson.htm or http://astro.temple.edu/~dhill001/trianglearea/trianglearea.html
Personalization: I had a ballet performance of the
Nutcracker on saturday and sunday and here's a picture from Snow which comes right before the Land of Sweets!
 Reminder: Arash you are next!
Reminder: Arash you are next!

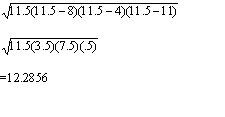

2 Comments:
ooo kool!! where r u in the pict??? front and center i bet :D and nice blog..i especially lkd dat pict of hero lol helped me to visualize the man who saved us from solving lengthy equations ;p
you're my favorite ballerina...pretty tutus!
Post a Comment
<< Home