4-6: Inverse Trigonometric Relation Graphs

Chapter 4 Section 6: Inverse Trigonometric Relation Graphs

Main Concepts:

Graphs and Principal Branches:

The Definition of arcsin, arctan, and arccos:
Using sine as an example, arcsin x means any of the angles whose sine is x. Arctan and arcos have the same meaning. The problem with this is that the entire graph will not be a function because it does not pass the vertical line test. Therefore, you must take the principal branch of the graph to make it a function. An inverse trigonometric function is a reflection of one branch of the graph across the line y=x. In choosing the principal branch, you must:
1. Include the entire domain
2. Include the origin, or make it as centrally located as possible
3. It must be a function
4. It should be a continuous graph
5. Choose the positive branch if possible

The Graph of Arcsin:The Graph of Arccos:The Graph of Arctan:

The principal branches of the graphs:

• The Graph of Inverse Sine: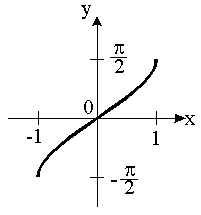Keep in mind that the domain of the original sine function becomes the range of its inverse. Domain: [-1, 1]; Range: [o, π]; In reference to the (u,v) coordinate system: Quadrants I and II

• The Graph of Inverse Cosine:

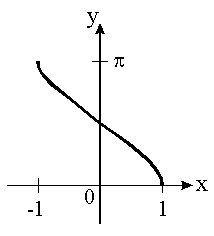
Domain: [-1, 1]

Range: [-π/2, π/2]

Quadrants I and IV

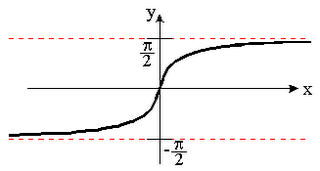
• The Graph of Inverse Tangent:

Domain: all real numbers

Range: [-π/2, π/2]

Quadrants I and IV

• For the other inverse trigonometric functions:

• Inverse cotangent:

Domain:[-1, 1]; Range: [0, π]; Quadrants I and II

• Inverse secant:

Domain:the absolute value of x ≥ 1; Range: [0, π] and y ≠ π/2; Quadrants I and II

• Inverse cosecant:

Domain:the absolute value of x ≥ 1; Range: [-π/2, π/2] and y ≠ 0; Quadrants I and IV

You can graph inverse trigonometric functions in parametric mode:

x1= sin (T)

y1= T

x2= cos (T)

y2= T

x3= tan (T)

y3= T

This will give you the entire graph of the inverse; even when it is not a function.

When you are in function mode and you graph these, your calculator will give you the graph of a function (like the restricted graphs shown above).

Exact Values of Inverse Circular Functions:

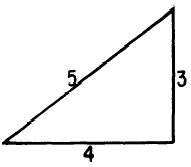
You can geometrically figure these types of problems out by creating a triangle from the given information.

Such as with cos(sin^/1(4/5))

• you can create a 3-4-5 triangle with this information and figure out the cosine of this angle is 3/5

• <--- The angle we are referring to.

• Sine= opp/hyp, so 4/5 and then you fill in the remaining side. Cosine= adj/hyp, so 3/5

• The Composite of a Function and Its Inverse Function:

f(f^-1(x)) = x and f^-1(f(x)) = x

This holds true only if the "x" is within the range of the outside function and the domain of the inner function.

Example Problem:

Using the concept that we learned about composite functions and their inverse functions:

Remember, f(f^-1(x)) = x and f^-1(f(x)) = x.

Problem:

cos(cos^-1(3/5)) = ?

3/5 is within the range of the outside function and the domain of the inside function, so the answer is 3/5.

For sin(sin^-1(4/5))

the answer is 4/5 because 4/5 is within the range of the outside function and the domain of the inside function.

For sin(sin^-1(5/3))

5/3 is not within the domain of the inside function. The domain of this function is [-1,1] and 5/3 is greater than one. Therefore, sin(sin^-1(5/3)) ≠ 5/3

Link for additional reference: http://www.sparknotes.com/math/precalc/trigonometricfunctions/section4.rhtml

This is my favorite painting...

****Reminder: Debby! You're up again! Good Luck!!!