5.4 Composition of Ordinates and Harmonic Analysis
Hey guys! Welcome back from Thanksgiving break-what better way to start off the week than with a lesson on combining sinusoidal graphs with different periods?!
Let's start with breaking down the title...
Composition of ordinates: Adding or multiplying sinusoids
Harmonic analysis: Finding the parent sinusoids from the new sinusoid
COMPOSITION OF ORDINATES
Some general tips to remember when drawing the new graph:
1. The points that make up the new graph are found by either adding or multiplying the corresponding ordinates of the parent graphs, meaning that for each x or theta value that we choose, we must find the y-value. (We can also look at this as adding or multiplying amplitudes)
2. Look for points that are easily identifiable.
3. Focus on the zeros, maximums, and minimums of the smaller graph; work off of the big graph using these points.
Differentiating between the Sum of Two Sinusoids and the Product of Two Sinusoids:
Sum: There is no constant sinusoidal axis, but the larger parent graph becomes the midpoint of the new graph (inner curve).
In this graph, the parent curves are in red and blue and the resulting curve is in green, representing the sum of the two parent sinusoids.
1. The points that make up the new graph are found by either adding or multiplying the corresponding ordinates of the parent graphs, meaning that for each x or theta value that we choose, we must find the y-value. (We can also look at this as adding or multiplying amplitudes)
2. Look for points that are easily identifiable.
3. Focus on the zeros, maximums, and minimums of the smaller graph; work off of the big graph using these points.
Differentiating between the Sum of Two Sinusoids and the Product of Two Sinusoids:
Sum: There is no constant sinusoidal axis, but the larger parent graph becomes the midpoint of the new graph (inner curve).
In this graph, the parent curves are in red and blue and the resulting curve is in green, representing the sum of the two parent sinusoids.
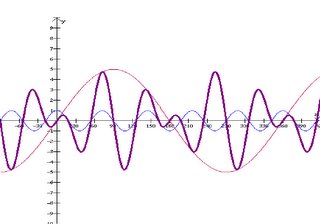
Product: There is a constant sinusoidal axis, and the larger parent graph becomes the boundary of the new graph (envelope curve).
In this graph, the parent curves are in red and blue and the resulting curve is in purple, representing the product of the two parent sinusoids.
HARMONIC ANALYSIS (EYE TO EYE WITH THE MONSTER)
The Procedure:
1. Determine whether or not it is Product or Sum based on whether or not it has a constant sinusoidal axis.
2. Draw the larger curve and determine its equation.
If it is a product...
3. Find the midpoint of the larger cycle and look for symmetry. If the graph is symmetrical around the midpoint, this means that both trigonometric functions are the same.
4. Count the contact points and then subtract 1, in order to get the number of cycles. Use this number as the coefficient of x or theta in the second half of the equation. (For example, this number would be placed where the 11 is: y=5sinxsin11x)
Hint: The 5 in this equation represents the dilation of both functions in the product; the amplitude of the shorter-cycle fucntion is always 1
If it is a sum...
3. Determine whether the sum is *sin + cos, cos + sin, sin + sin, cos + cos* by looking at the origin for symmetry.
4. Find the amplitude of the smaller curve by finding how far above and below the big curve it reaches. (This number will be placed where the 2 is: y=4costheta + 2sintheta)
5. Find the contact points the same way, subtracting 1 to get the number of cycles, and then before inserting this number as the coefficient of theta/x in the second part of the equation, multiply it by the coefficient of theta/x in the first part of the equation. (If we are finishing teh equation y=4cos45theta +2_____ and we have 10 cycles, the equation becomes y=4cos45theta + 2sin450theta)
Example Problem:
Harmonic Analysis: Find the particular equation for this graph.
1. Because we can see that this graph has a constant sinusoidal axis, we know that it is a Product.2. Draw the larger curve and determine its equation.
If it is a product...
3. Find the midpoint of the larger cycle and look for symmetry. If the graph is symmetrical around the midpoint, this means that both trigonometric functions are the same.
4. Count the contact points and then subtract 1, in order to get the number of cycles. Use this number as the coefficient of x or theta in the second half of the equation. (For example, this number would be placed where the 11 is: y=5sinxsin11x)
Hint: The 5 in this equation represents the dilation of both functions in the product; the amplitude of the shorter-cycle fucntion is always 1
If it is a sum...
3. Determine whether the sum is *sin + cos, cos + sin, sin + sin, cos + cos* by looking at the origin for symmetry.
4. Find the amplitude of the smaller curve by finding how far above and below the big curve it reaches. (This number will be placed where the 2 is: y=4costheta + 2sintheta)
5. Find the contact points the same way, subtracting 1 to get the number of cycles, and then before inserting this number as the coefficient of theta/x in the second part of the equation, multiply it by the coefficient of theta/x in the first part of the equation. (If we are finishing teh equation y=4cos45theta +2_____ and we have 10 cycles, the equation becomes y=4cos45theta + 2sin450theta)
Example Problem:
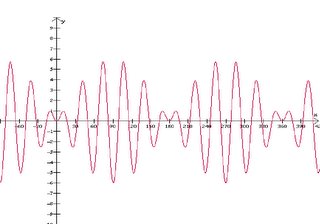
Harmonic Analysis: Find the particular equation for this graph.
2. Next we determine an equation for the larger curve, whose trigonometric function we know to be sin, because the graph goes through the origin. We also know that it has an amplitude of 6, so its equation is: 6sintheta
3. We can see that the graph is symmetrical at x=180, so we know that the second trigonometric function in our equation will be sin, the same as the first.
4. Now, we have to count the number of cycles, which we find by counting the contact points and then subtracting 1. There are 12 contact points, so there are thus 11 cycles. We insert this value into the second half of our equation: sin11theta
5. We are now ready to combine the two halves of the equation!! When we multiply our answer from #2 with our answer from #4, we get the equation: y=6sinthetasin11theta
For More Information:
If you'd like to get more information on this topic, check out this site: http://www.keymath.com/x7188.xml
It is actually a link off of a website that is all about our textbook; it offers extra information pertaining to the subjects we cover, so you could use it as a resource throughout the year. Hopefully the author included (Surprise?!) on the exciting website problems.
Nick...YOU'RE UP NEXT!! Just in case you guys are confused as to why we're going out of order, don't forget that I'm subbing for Natalie.
This is a picture of my sister and me with my cousin, Tamar. She's 10 years old, and she's an amazing gymnast. This picture was taken during the summer after my 9th grade year in her backyard in Cheyenne, Wyoming.



1 Comments:
cute picture!
Post a Comment
<< Home