Prep Precalculus D 2006-07

Lesson for chapter 4-4: Arcsine, Arctangent, Arccosine, and Trigonometric Equations
This section is

about...
1) solving for the theta or "x" (all the angles that have the same sin value, tan value or cos value)
2) memorizing the equations for arccos, arcsin and arctan
3) being able to visualize the reference triangles involved

Okay, so to review, we learned that to solve...
cos(x)=a
1st step) you have to use the arccos --> x= arccos(a)

2nd step) then simplify to what arccos actually means --> x= +/- inv. cos (a) + 2 pi(n)
What does it mean?
The arccos means that you solve for all the angles "x" that have a ratio "a" of adjacent/ hypotenuse in their reference triangles.
The reason we have the "+/-" (plus or minus) before the "inverse cos" is because... there are two angles on the "u, v coordinate system" that have the same ratio of adjacent leg/ hypotenuse.

For example: If the problem was, cos(x)=3/5... you can picture two reference triangles that yield this same ratio of adjacent side 3 and hypotenuse 5... It would look like this..

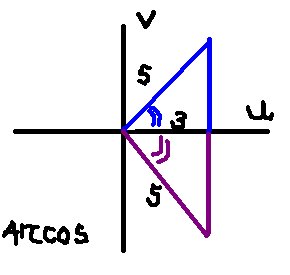
The blue reference triangle: adj 3 & hyp 5 (ratio of 3/5) and the purple ref triangle: adj 3 & hyp 5 (ratio of 3/5)
Blue angle= inv. cos (3/5)
purple angle= negative inv. cos (3/5)
Now add periods (2pi or 180 degrees) to both blue and purple angles to get the angles in all the other periods.
Equation for arccos:

x= +/-inv. cos (3/5) +2pi(n)
Note: the (3/5) is the number ratio of adj/hyp

Also note: REMEMBER to be in the right MODE, use radian mode for pi's and x's. Use degree mode for theta's and substitute 360 for 2pi.

Arcsine
arcsin (x) means all the angles whose sin is x (or all the angles that have the same ratio of opposite/hypotenuse) So, when you think about sin(x)=(3/5)...draw it out like this...

To get the angl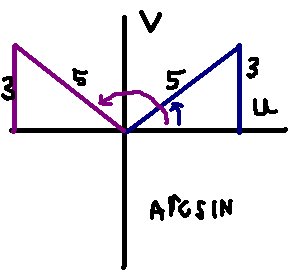es whose sine is 3/5, you can draw 2 triangles... the blue reference triangle: opp side of 3 & hyp 5.
the purple ref triangle: opp side of 3 & hyp 5
This means that the blue arrow and the purple arrow represent 2 angles whose sin ratios = 3/5.
Blue angle= inv. sin (3/5)

purple angle= pi - inv.sin(3/5)
To get the purple angle you subtract the blue angle from pi (180degrees) because the ref angles are equal. Now add periods (2pi) to both the blue and purple angle to get the rest of the angles in all the other periods.
Equations for arcsin: x=inv.sin(3/5) +2pi(n)

or ... x= pi -minus inv.sin(3/5) + 2pi(n)

Arctan
Arctan(x) means all the angles whose tan is x.
So for the problem: tan(x)=3/5, think about all the angles whose opp = 3 and adj=5

First draw the reference triangles...

To get the angles whose tangent is 3/5, you can draw two triangles–
1)the blue ref triangle with an opp side 3 & adj side 5
2)the pink ref triangle with an opp side -3 & adj side -5 (this ratio of -3/-5 simplifies to 3/5)
blue angle= inv.tan (3/5)
to get to the pink angle you have to add pi(180 degrees)...
pink angle= pi + inv.tan(3/5)
to get to the blue angle again by going around the circle, you add pi.
Next blue angle= 2pi + inv.tan(3/5)
Therefore, you get to the next angle by adding pi, which is the period of the tan graph!
Equation for arctan: x= inv.tan (3/5) + pi(n)

note: (3/5) is the ratio for this specific problem

This makes sense when looking at the tangent graph because when you draw the line at y=3/5, there is only one intersection period of pi(180deg).
(sorry the pictures don't want to upload at all)

Whereas, in the sine (red) and cosine graph (blue) there are two intersections per period of 2pi(360deg), reflected in the two angles per period of 2pi for which the ratios are the same in the u, v coordinate plane.


Note: for all of these arc equations, you can solve for degrees by using 360degrees instead of2pi and 180degrees instead of pi. and again CHECK THE MODE
Interval Notation: another way to write the domain
A Closed interval
1)includes the end points
2) greater than or equal to / less than or equal to
3)is written with [brackets]
4)for example [0,4] means 0
An Open Interval
1)does not include the end points
2) > or <>

3) is written with (parentheses)

4) For example (o, pi) means 0

Note: You can combine the closed interval and open interval:
example: (0,2] ...this means x is greater than 0 and less than or equal to 2
New Symbol: *i can't insert the symbol...so it basically looks like a flattened capital e*

What does it mean? it means that x is in the domain of/ "in the element of"...
example: X *special symbol*[-400,3) ...means that x is greater than or equal to -400, and x is less than 3.


Practice Problem
Solve the equation 10 sin (x- .2) = -3 algebraically for x in the domain [0,4pi]. Show that your answers correct on a graph.

10 sin (x - .2) =-3

To solve for x, you can divide by 10 to isolate x on one side of the equation.
sin ( x-.2) = -.3 Take the arcsin of both sides to cancel the sin from the right side and further isolate the x.
(x- .2) = arcsin(-.3) Now, add the .2 to each side.
X = .2 + arcsin (-.3) Substitute the inv. sin equivalent for arcsin
x= .2 +sin (-.3) +2n or x=.2+ (-sin(-.3) +2n Simplify
x= -.105.. +2n or x= 3.646 +2n Now, find the solutions within the domain 0#x#4
x= 3.646, 6.178, 9.929, 12.462
To check your results, you can graph the original equation: y=10sin(x-.2) and what you set it equal to: y=-3 into your calculator graph. Now, find where they intersect in the given domain using the "calc" program.
Links for further information on inverse trig functions...

http://www.themathpage.com/aTrig/inverseTrig.htm
Celene!!! You are next to blog!
i really want to finger paint like this little girl. I would definitely choose it as my major in college.