Chapter 3 Test Topics

Here’s a list of topics for Thursday’s test:

Precalculus Chapter 3 Test Topics:
Radians to degrees (special angles)
Degrees to radians (special angles)
Sketch a sinusoidal graph given an equation
Demonstrate the concept of radians by wrapping an axis around a circle
Sketch an angle in radians
Show the steps necessary to convert from radians to degrees, or vice versa
Position/Locate a radian angle
Inverse trigonometric functions
The meaning of arccosine
The definition of arccosine
A visual interpretation of radians and arclength
Determining a radian measure of an angle
Determining a sinusoidal equation from a graph – sine and cosine
Word problem! Work with the given situation graphically, numerically and algebraically.

That’s it! The format is as expected – ½ calculator, ½ Non-Calculator. I’ll be in my classroom on Wednesday after school and before school on Thursday. I’ll also be available online later on Wednesday evening. If you have specific questions Wednesday night, email me!

See you in class!

"Sometimes when I get up in the morning, I feel very peculiar. I feel like I've just got to bite a cat! I feel like if I don't bite a cat before sundown, I'll go crazy! But then I just take a deep breath and forget about it. That's what is known as real maturity."
- Snoopy

3-7; Sinusoidal Functions

Chapter 3, Lesson 7: Sinusoidal Functions as Mathematical Models

Main Objective: "To write an equation using sine or cosine functions and use the equation as a matematical model to make predictions and interpretations about the real world"

Using what we have learned in past chapters:

y=C + A(Sin or cos) (B(x or theta - D))

*use "X" when in radian mode
*use "theta" when in degree mode

C= sinusoidal axis (vertical translation)
A= amplitude (vertical dilation)
B= 360/period (horizontal dilation)
D= phase displacement (horizontal translation)

Radians converted to degrees: 180/pi
Degrees converted to radians: pi/180

Tip: After looking at the word problem decide if you should use sine or cosine.

Use sine: when you are dealing with the location of the midpoint of a graph
Use cosine: when you are dealing with the maximum of a graph

Tip: After looking at the word problem decide if you should use radians or degrees:

*Use radians: when you want to eliminate the confusion of having different units

Summary:

This lesson basically combines the things we have learned about sin and cos functions with what we have learned about radians and degrees and puts them in a real world situation, using circular graphs to depict situations that we need to translate into sinusoidal functions.

There are 2 graphs you might have to use in word problems:

A circle with P= point on outer rim, r= radius, d= distance to ground (ex. wheel problems) and the sinusoid graphs (sin and cos) we have learned about

Example:

Suppose that the waterwheel in the figure rotates at 6 revolutions per minute. Two seconds after you start a stopwatch, point P on the rim of the wheel is at its greatest height, d=13 ft, above the surface of the water. The center of the waterwheel is 6ft above the surface.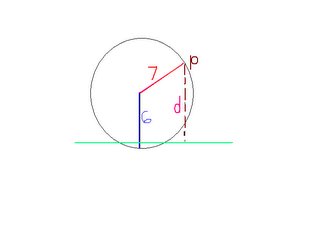

a. Sketch the graph of d as a function of t since you started the stopwatch.

b. Assuming that d is a sinusoidal function of t, write a particular equation.

c. How high above or below the water's surface will P be at time t=17.5 sec?

d. At what time (t) was point P first emerging from the water?

Answer:

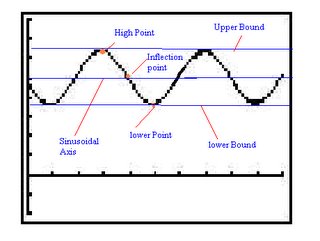
a. From the information we are given, you can tell that the sinusoidal axis is located at d=6 (this is the center of the waterwheel). Because you know the sinusoidal axis you can figure out the high and low points by adding and subtracting the amplitude (7).

6+7= 13 (high point)

6-7= -1 (low point)

Sketch the high point at t=2 because point P is at its maximum after 2 seconds

Because the waterwheel rotates at 6 revolutions per minute, the period is 60/6= 10 seconds, or 1 revolution in 10 seconds. This means you would mark the next high point at t=2 + 10=12

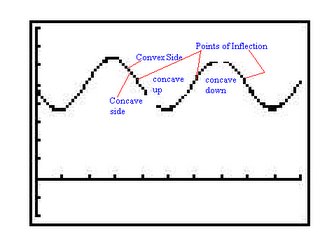
*Continue by marking a low point halfway between the two high points, and mark the points of inflection on the sinusoidal axis halfway between each consecutive high and low*

The graph should look like the following:

b. Remember: d=C+AcosB(t-D) As we can see from the graph, C=6, A=7, and D=2

Because the period of this sinusoid is 10, using radians the "B" would be calculated as 10/2(pi), which equals 5/(pi)

*Don't forget*- B is the RECIPROCAL of the horizontal dilation, therefore B= pi/5

Using the formula above you would write the answer as d=6+7cos((pi/5)(t-2))

c. Set the window on your grapher to include 17.5. Then trace or scroll to this point. By looking at the graph you can determine that d= -.6573 and is going up.

d. Point P is either submerging into or emerging from the water when d=0. At the first zero the point is going into the water. At the next zero, the point is emerging. Using intersect or zeros on your calculator you will find points at:

t= 7.8611...rounded to 7.9 seconds

For Additional Problems or help with Sinusoids in general (which can help you with sinusoidal model problems) go to http://www.nsa.gov/teachers/hs/trig16.pdf

This is a picture of my puppy Luna, who I'm raising to be a Guide Dog.

Landry, you are next! Good Luck!

3.6 Inverse Circular Functions

Okay Gang! I get the pleasure of explaning to you the joys of Inverse Circular Funtions. Get ready for a mystical adventure!

Arccosine
The Arccosine is the same as (+/-) cos-1x. it includes all arcs whose cosine is the given numer, x, and it gives you all the other values that the calculator does not tell you. Its equation is

Arccos x = ± cos-1 + 2πn

“n” determines the amount of periods that you wish to calculate. For every value you put in place of n, you move left or right that many periods. N must be an integer, but it can be negative. A negative n value means a movement along the x axis.

The "± cos-1" portion is also known as the principal value of the relation. this is the value the calculator gives you.


Using a Graph
A sinusoidal graph can be used to determine the value(s) of the Arccos. Simply plot the sinusoid…

y= cos 2x + 1

and a line at which value you would like to calculate the arccos.



y = .9

to visually get the values for Arccosine.



Each point where the two lines intersect represent an arccos value.

Solving Algebraically
If you are given two equations, one cosine and one line, you can algebraically solve for the arccosine value. Simply put the two equations into the same equation, and solve.

Sample Problem
This sample problem relates to algebraically solving for the arccosine value.

Y1 = 9 + 7 cos (2π/13)(x-4)
Y2= 5

To slove, make both sides equal.

5 = 9 + 7 cos (2π /13)(x-4)

Subtract 9 from both sides.

-4 = 9 + 7 cos (2π/13)(x-4)

Divide both sides by seven.

( -4 / 7) = cos (2π/13)(x-4)

Use the Arccosine to get rid of the cos.

Arccos (-4/7) = (2π/13)(x-4)

“Arccos” can be replaced with “± cos-1 + 2πn”

± cos-1 ( -4/7 ) + 2π n = ( 2π / 13)( x-4)

Multiply both sides by the reciprocal of ( 2π / 13).

± ( 13 / 2π ) [cos-1 ( -4/7 ) + 2π n] = ( x-4)

Distribute the ( 13 / 2π )

± ( 13 / 2π ) cos-1 ( -4/7 ) + 13n = x-4

Add four.

± ( 13 / 2π ) cos-1 ( -4/7 ) + 13n + 4 = x

Now that you have the simplified expression, plug into your calculator and solve. Make sure you are in radian mode!

8.508, -.508

Additional Recources

http://www.pinkmonkey.com/studyguides/subjects/trig/chap6/t0606101.asp


Check This Out!
This Man's name is Bill Clements, a bass player from Michigan who lost his right hand in an industrial accident. He spent a few years redeveloping his style and now he manages to play his instrument using only his left hand.

http://www.youtube.com/watch?v=k5ThulqDmKc

Allison! You're Next.

Wednesday's Quiz Topics

Here’s a list of topics for Wednesday’s quiz:

Precalculus Quiz 3.3-5 Topics
Radians
Convert Radians to Degrees
Convert Degrees to Radians
Sinusoids (radians)
Sketch a sinusoidal graph from an equation
Determine a sinusoidal equation from a graph
Graphs of tangent, cotangent, secant and cosecant
Identify transformations of a sinusoid
Identify characteristics of a sinusoid
Analyze a sinusoidal situation given specific information (yes, the ever-present word problem!)

That’s it. I’ll be in early on Wednesday…

"Optimists are right. So are pessimists. It's up to you to choose which you will be."
- Harvey Mackay

3.5 Circular Functions

Main Concepts:

Circular Functions: Periodic functions whose independent variable is a real number without units

We are accustomed to graphing period functions whose independent variable is theta, meaning theta ------> degrees

we will now graph periodic functions whose independent variable is a unitless real number, meaning x ------> radians

The numbers are unitless because a radian is a ratio in which the units cancel:

Radian=Radius/Circumference

Thus, using the common degrees to radian conversions (90=pi/2, 180=pi, 360=2pi etc.) we can label our independent variable axis (now x as opposed to theta) and find the period and phase displacement.

Note: The y-axis does not change because only the independent variable axis is measured in radians. Therefore, the period and phase displacement are notated differently, but the amplitude and sinusoidal axis remain the same.

Circular Function

Trigonometric function

(Blue=cos, Red=Sin)

As shown by these two graphs, circular functions are equivalent to trigonometric functions in radians. Thus, assuming that the terminal point of an arc on the unit circle is at (u,v) and the arc's length is x,

sin x=v cos x=u

tan x=sin x/cos x cot x=cos x/sinx

sec x=1/cos x csc x=1/sin x

Example Problem:

Given the equation y=3cos6(x-20)-2, find the sinusoid's amplitude, phase displacement, period, and sinusoidal axis.

1.First we must determine which of these sinusoidal characteristics is affected by the fact that the graph is in radians and not degrees.

Because the amplitude and sinusoidal axis are determined by the y-axis,

Amplitude=3

Sinusoidal axis: y=-2

2.We must then go about finding the phase displacement and the period.

In degrees, Period=360/6

Since the argument is measured in radians, Period=2pi/6

In degrees, Phase displacement=20

Since the argument is measured in radians, Phase displacement=20 radians

For more information:

http://colalg.math.csusb.edu/~devel/precalcdemo/circtrig/src/trgraphs.html

If you guys are ready for a good time, check out this music video. My French AP Lit. class is the man's new fan club...keep watching until it gets to the random flashing lights in the background.

http://video.google.com/videoplay?docid=2274083658088737981&q=Jacques+Brel+Madeleine

Good luck Henry...YOU'RE UP NEXT!

3.4 Radian Measure of Angles

Hey everybody! Here is the lowdown on radian measures of angles!

The Main Concepts are...

The relationship between pi and a circle is that the circumference divided by 2 times the radius = pi. The radian is the length of the radius of the circle. The relationship between a radian and a circle is that pi is equal to 3.14...radians that wrapped around the circle, like this:

This graph is supposed to be on the UV axis, with the radius at (0,0).

Where the radians intersect the circle creates an angle with the center the circle. The angles would be same in all circle, for the radian is proportionate circumference. The angles will look like this:

Where 1, 2, and 3 stand for the angles created by the number of radians. The angles made by the radian will always have the same length in the arc as the legs of the angle, and can be described by the formula A1/R1 = A2/R2, because both equations are equal to 1. The angle the is created by the radian

subtends, or cuts off, a fragment of the circle which is the length of the radian.

The measure of a radian is always the arc length divided by the measure of the radius. Ex: if the arc were 3 units and the radius were 1.5 units, the radian would be 2.

If you know the radian measure of an angle, it is possible to express the measure that way, using (while in RADIAN mode) the small r (under 2nd, APPS).

When you know the angle measure in degrees and want to find the measure in radians, the formula is pi/180 degrees. In order to find the degree measure when you have the radian measure, the formula is 180 degrees/pi.

The most common radian measures are those of 30, 60, 90, 45, 180, and 360 degrees. The radians are exactly pi/6, pi/4, pi/3, pi/2, pi, and 2pi respectively. These number come from the number of degrees in pi, or 180, divided by the given degree. Ex: 180/30 = 6, which is in its corresponding radian formula. To find the number of full revolutions, simply divided 360 degrees by the given angle measure. Ex: 360/30 = 12, thus a radian with that measure goes around the circle 12 times evenly.

Example Problems!

1. find the exact radian measure of 45 degrees.

To solve this, use the formula of ( pi/180 ) x 45. The answer is pi/4.

2. Find the exact degree measure of 3pi/4.

To solve this, use the formula of ( 180/pi ) x (3pi/4). When you multiply it out, the formula is 540pi/4pi, which simplifies to 135 degrees.

3. Find the exact value of sin pi/3.

To solve this, use the change the radian measure of the angle to degrees, which is 60 degrees. Then solve like we have previously, using the 30, 60, 90 triangle.

If you need more info on this topic, check out http://aleph0.clarku.edu/~djoyce/java/trig/angle.html

TARA YOU ARE NEXT!!! WOOT!

And finally, in case you guys need some inspiration in your mathy endeavours, here is my masterpiece:

And if you wanted real entertainment, check out http://youtube.com/watch?v=9aizQBcJFf8.

Thursday's Quiz

Here’s a list of topics for Thursday’s quiz:

Precalculus Quiz 3.1-3 Topics
Sinusoids:
Cycles
Periods
Phase displacement
Critical points
Points of inflection
Concavity
Sketch a sinusoidal graph from an equation
Determine a sinusoidal equation from a graph
Graphs of tangent, cotangent, secant and cosecant
Identify transformations of a sinusoid
Identify characteristics of a sinusoid
Analyze a sinusoidal situation given specific information (yes, the ever-present word problem!)

That’s it. I’ll be in early on Thursday…

"There is nothing noble in being superior to someone else. The true nobility is in being superior to your previous self."
-Hindu Proverb

Lesson 3-3

Hey im excited, My 1st Blog
3-3- Graphs of Tangent, Cotangent, Secant, and Cosecant Functions

Main Concepts

3-3 objectives is to allow us to visualize the graphs of Tangent, Cotangent, Secant, and cosecant functions, and show the behaviors and details of the functions.

1- Tangent Graph

• Tan (X)=Sin(X)/Cos(X) values of the Sin(X) is the values of X-intercept. So, If Sin(X)=0 then the Tan(X) is 0. Cos(X) is the value of Y-intercept. If Cos(x)=0, then Tan(X)=undefined. If Sin and Cos are equal then Tan is 1 and if they are opposites then Tan is -1.

• Vertical Asymptote, every time the function is undefined

• Period length is 180 degrees.
  

Cotangent Graph

• Cot(X)=Cos(X)/Sin(X), all the details of Tan(X) is oppisite for Cot(X).
  

• There is an Asymptote, everytime the sin(X) is 0 because it is undefined.
  

• Period length is 180 degrees.

2- Secant Graph

• Sec(X)=1/Cos(X)
  
  
• The reciprocal of the Cosine function is the Secant function. When the Cos(X)=0, then the secant is undefined and it has an Asymptote.

• When Cosine value is larger, then the Secant value is smaller, and vica versa. The Period length is 360 degrees. Origin is at 1.
  

3- Cosecant Graph

• Csc(X)=1/Sin(X)

• Sin and cosecant are reciprocals, and as the cosecant gets bigger, the Sin gets smaller, and vice versa.

• Asymptote occurs as the Sin is 0 and the Cosecant becomes undefinded. The Period length is 360 degrees. Origin is at 1.

Example Problem

Problem- Graph the function of Sin(X). Use the fact that Csc(X)=1/Sin(x) to sketch the graph of the cosecant fuction. Describe the function and the asymptote.

Solution- 1st-Sketch of the Sin(X) graph

• 
  

2nd- sketch the Csc(x) graph

• 

• 
  

1. Where the sine function is 0, the cosecant function is undefined and has a vertical asymptote.When the sine function equals 1 and -1, so does the coseacant function. As the sine function get smaller, the coseacant function gets bigger.

Additional Resources

http://home.alltel.net/okrebs/page74.html is an internet site that will help you clear any extra questions up about these concepts.

Claire your up next;Have fun with your first blog and Good luck

My personalization Section: I have a Joke for everyone

A doctor, a lawyer, a little boy and a priest were out for a Sunday afternoon flight on a small private plane. Suddenly, the plane developed engine trouble.

In spite of the best efforts of the pilot, the plane started to go down. Finally, the pilot grabbed a parachute, yelled to the passengers that they had better jump, and bailed out.

Unfortunately, there were only three parachutes remaining.

The doctor grabbed one and said "I'm a doctor, I save lives, so I must live," and jumped out.

The lawyer then said, "I'm a lawyer and lawyers are the smartest people in the world. I deserve to live."

He also grabbed a parachute and jumped.

The priest looked at the little boy and said, "My son, I've lived a long and full life. You are young and have your whole life ahead of you. Take the last parachute and live in peace."

The little boy handed the parachute back to the priest and said, "Not to worry, Father. The 'smartest man in the world' just took off with my back pack."

Chapter 2 Test Topics

Here’s a list of topics for Thursday’s test:

Precalculus Chapter 2 Test Topics:
Sketch an angle given a point on the terminal side or a measurement in degrees.
Determine the reference angle’s location and measure.
Determine the six trigonometric functions for the angle.
Describe transformations to a trigonometric graph and determine the resulting function.
Determine trig functions based on right triangles.
Determine the principal branch of a trigonometric function.
Describe the characteristics of a principal function (one-to-one).
Discuss the reason for a principal branch.
Sketch a graph of a function given a description.
Determine type of function based on graph.
Find trigonometric functions with your calculator.
Determine reference angles and discuss their relationship to primary angles.
Triangle word problems – determine angles and sides.

That’s it! The format is as expected – ½ calculator, ½ Non-Calculator. I’ll be in my classroom until 3 on Wednesday and before school on Thursday. I’ll also be available online after Back to School Night on Wednesday.

See you in class!

Chapter 3 Section 2: General Sinusoidal Graphs

Main Concepts:
Period: the number of degrees per cycle
Frequency: the number of cycles per degree

General Sinusoidal Equation:
y= C+ A cos B(θ-D)

or

y= C+ A sin B(θ-D) where...

·│A│ is the amplitude (A is the vertical dilation, which can be positive or negative)
The amplitude is the distance from the sinusoidal axis to a max. point or a min. point

· B is the reciprocal of the horizontal dilation
When you multiply by θ it dilates by a factor of 1/B

· C is the location of the sinusoidal axis

· D is the phase displacement (horizontal translation)

You can calculate the period from the value of B by:

Period= 360/B

or

B= 360/ period

PROPERTY: Period and Frequency of a Sinusoid:
For the general equations y= C+ A cos B(θ-D) or y= C+ A sin B(θ-D)

period= 1/│B│(360)

and

frequency= 1/period = │B│/(360)

Graphing Sinusoids and finding their equations:

Concave: hollowed out side (holds water)

Convex: bulging side (spills water)

Point of Inflection: occurs where a graph stops being concave one way and starts being concave the other way.

Upper Bound: the line through the "high points" of the graph

Lower Bound: the line through the "low points" of the graph

Critical Points: the "high points" and "low points" of the graph (max. and min.)

Example Problem:

You should be able to determine the amplitude, the sinusoidal axis, the period, and the phase displacement from an equation.

Equation: y= 3+ 2 cos 4 (x-20)

To figure out these values refer to the equation y= C+ A cos B(θ-D)

Amplitude (A)=2

Sinusoidal axis (C)=3

Period (360/B)=90

Phase displacement (D)= 20

Graphed:

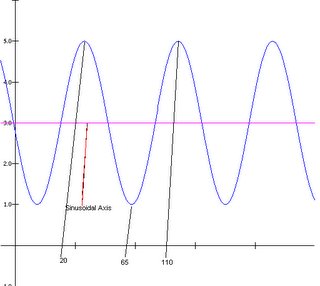New max on graph becomes 20 then add the period to equal the next max at 110. 65 is the middle point between 20 and 110. The sinusoidal axis is at 3. To get the amplitude go up the amplitude (2) up and down from the sinusoidal axis and those points become the max. and min.

Additional resources:
http://www.math.duke.edu/education/ccp/materials/precalc/singraph/contents.html


Check out this! : http://www.youtube.com/watch?v=lTYCi3wP-W8

It's a spoof of Snakes on a Plane that my ballet teacher and a group of people made.

Reminder: Arash you are next! Good luck.

Chapter 2 Section 5

Inverse trigonometric Functions and Triangle Problems


Objective: given two sides of a right triangle or a side and an acute angle, find measures of the other sides and angles.


Inverses of Trigonometric Functions
To find the measure of an angle when its function value is given, you could press a keys in your calculator, for example, if cos θ = 0.8, then you would press cos-1 0.8 = 36. 8698


For the symbol cos-1, you would say “inverse of cosine 0.8.”
Note: it DOES NOT mean the -1 power of cos, which is the reciprocal.


The domain of the inverse is the range of the original function and the range for the inverse is the domain of the original.


Trigonometric functions are periodic. They are not one-to-one functions.
Principal Branch: for each trigonometric function there is a principal branch of the function that is one-to-one and includes angles between 0º and 90º. It includes the entire range of original function.


Definitions of the inverse trigonometric function:
If x is the value of a trigonometric function at angle θ, then the inverse trigonometric functions can be defined on limited domains.

θ = sin-1 x means sin θ =x and -90º < θ <>

θ = cos-1 x means cos θ =x and 0º < θ <>

θ = tan-1 x means tan θ =x and -90º < θ <>

Domain: x <90

Range : all real numbers

Right Triangle Problems

Example:

A ship is passing through the straight of Gibraltar. At its closest point of approach, Gibraltar radar determines that the ship is 2400 m away. Later, the radar determines that the ship is 2650 m away.
a. By what angle did the ship’s bearing from Gibraltar change?
b. How far did the ship travel between the two observations?

Solution:

a. Draw the right triangle and label the unknown angle θ.

By the definitions of cosine,

cos θ = adjacent/hypotenuse= 2400/2650

θ = cos-1 2400/2650 = 25.0876…º take the inverse cosine to find θ

The angle θ is about 25.09º

b. Label the unknown side d, for distance. By the definition of sine,

d/2650 = sin 25.0876…º

d = 2650 sin 250876...º = 1123.6102…

The ship traveled about 1124 m.

want to learn more about Inverse Trigonometric Funtions? go here: http://www.ugrad.math.ubc.ca/coursedoc/math100/notes/zoo/invtrig.html

I’ve always been known to ask stupid/weird questions (I’m sure Debby has heard this before): Do fetuses dream?

Anna, You're up next!!! Have fun :)

Chapter 2 Section 4

Chapter 2 Section 4: Values of the Six Trigonometric Functions

Ok guys St. Nick here to bring you the great Six Trig Functions. We already knew 3 of them. Sin ∂=(opp/hyp), Cos ∂=(adj/hyp), Tan ∂=(opp/adj). In this lesson we learn 3 more "Cofunctions" (The "CO" standing for Complementary) These functions are the reciprocal functions of the 3 that we know. The reciprocal to Sine is Cosecant (csc), Cosine is Secant (sec) and Tangent is Cotangent (cot). The equations are: csc ∂=(hyp/opp), sec ∂=(hyp/adj), cot ∂=(adj/opp). As you can see the actual equations are the reciprocals. You can think of it like this: cot ∂ = (1/tan ∂) or cot ∂ =(tan ∂)^-1.
The above equations are in Right Triangle Form. If Coordinate Form is given, it is still relatively easy to find the answers. When solving in Coordinate Form, remember that the Vertical Coordinate is v, the Radius is R, and the Horizontal Coordinate is u. So the sin ∂=(v/r), cos ∂=(u/r), tan ∂=(v/u), csc ∂=(r/v), sec ∂=(r/u), and cot ∂=(u/v).

When asked for exact values you should first find the r, and leave it in radical form, then go about answering the questions.

Above is a chart showing which formula to use in each situation.

Example Problem 1:
Find the exact values of the six trigonometric functions of an angle in standard position whose terminal side contains the given point (8,-5).
First find r. 8²+(-5)²= Square Root (89).
After finding r you can proceed knowing that u=8 and v=-5.

sin ∂=(-5/root(89))

cos ∂=(8/root(89))
tan ∂=(-5/8)
csc ∂=(root(89)/-5)
sec ∂=(root(89)/8)
cot ∂=(8/-5)

It may help if you visually if you graph this.

Sample Problem 2:
Find the value for the given trigonometric function (on your calculator).
cot 126˚. To find this you would have to find tan 126˚. Then either find the inverse (x^-1) or do 1/(tan 126˚). The answer would be -.7265

Here is a website with some additional resources.

http://people.hofstra.edu/faculty/Stefan_Waner/trig/trig2.html


If you want to see someone with great bartering skills then check this out. My friend showed me this and I thought it was pretty sweet.
http://oneredpaperclip.blogspot.com/2006/08/saskatchewans-bigggest-housewarming.html

Annie - have fun you're up next.

Thursday's Chapter 1 Test Topics

First, I've decided to postpone the Chapter 2 Application problem until next Friday (October 13th). Remember, your problems should reflect reality - if you need to restrict the domain of the problem, or somehow manipulate your scenario, by all means do so!

Ok, here are the topics:

Precalculus Chapter 1 Test Topics:
· Determine domain and range of a function from a graph
· Given a graph, sketch a given transformation
· Determine if an inverse relation is a function and justify
· Plot a function and its inverse relation using parametric mode
· “Shopping Cart”-type problem
· Determine the domain of a composite function consisting of restricted original functions
· Plot a composite function with a restricted domain
· Determine values of a composite function or explain why no value can be obtained
· Even and Odd functions
· Identify types of functions from equations and/or graphs
· Determine the inverse of a function and plot it on the same set of axes with the original function
· Explain the visual relationship on a graph between a function and its inverse


Mathematician or not?