2-3: Sine and Cosine Functions
Ok everyone, I was a little confused by this lesson, but I think I understand it now... Let's all cross our fingers here.
Periodic functions: a function whose values repeat at regular intervals.
 This is an example of a periodic function. The definition of a periodic function is: The function f is a periodic function of x if and only if there is a number p for which f(x-p) = f(x) for all values of x in the domain.
This is an example of a periodic function. The definition of a periodic function is: The function f is a periodic function of x if and only if there is a number p for which f(x-p) = f(x) for all values of x in the domain.A cycle on the periodic function is the actual part of the function that repeats (so on this example the loop-de-loop)
A period on the periodic function is the horizontal distance between the cycles. (so the distance between the highest points on two of the "ups" of this graph) (if that made any sense)
Sine and Cosine functions are both periodic functions.
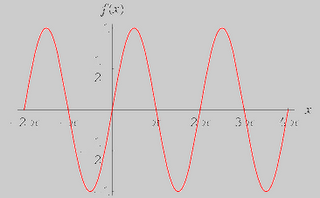
 This is an image of both the sine and cosine functions. The sine is red and the cosine is blue!
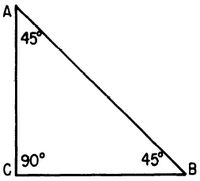
This is an image of both the sine and cosine functions. The sine is red and the cosine is blue!Sine and cosine can also be used in right triangles. We use SOH CAH TOA to remember how to find the sine, cosine or tangent. (SOH = sine: opposite/hypotenuse; CAH = cosine: adjacent/hypotenuse; TOA = tangent: opposite/adjacent).
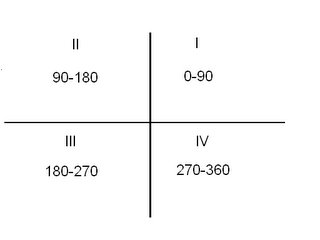
 But now we're using it on our UV coordinate plane. So if we were to try to find the sine of 120 degrees, we would first draw that on our coordinate plane, like so:
But now we're using it on our UV coordinate plane. So if we were to try to find the sine of 120 degrees, we would first draw that on our coordinate plane, like so: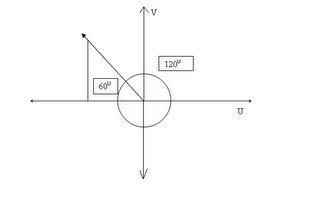
The definitions of the sine and cosine of any angle (in this case 120) are : Let (u,v) be a point r units from the origin on the terminal side of a rotating ray. If x is the angle in standard position to the ray, then sinx=v/r and cosx=u/r. Sinx will be positive in quadrants I and II, but it will be negative in quadrants III and IV (v is positive in 1st and 2nd quadrants and negative in the 3rd and 4th quadrants, divided by r which is always positive). Cosx will be the opposite. It will be negative in quadrants I and II and negative in quadrants III and IV. (u is negative in the 1st and 2nd quadrants and positive in the 3rd and 4th quadrants/r which is always positive)
 As the ray goes around the coordinate plane, the value of r is changing. At v=0, sinx=0 and at v=90, where r is equal to v , sinx=1. Also, sin180=0 and sin270=-1. As the ray circles the coordinate plane, the values are repeated, creating the periodic function.
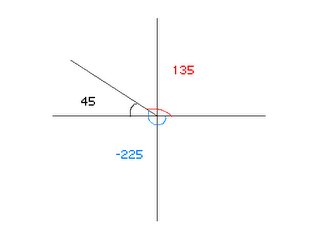
As the ray goes around the coordinate plane, the value of r is changing. At v=0, sinx=0 and at v=90, where r is equal to v , sinx=1. Also, sin180=0 and sin270=-1. As the ray circles the coordinate plane, the values are repeated, creating the periodic function.Example problem: Draw a 147 degree angle in standard position. Mark the reference angle and find its measure.
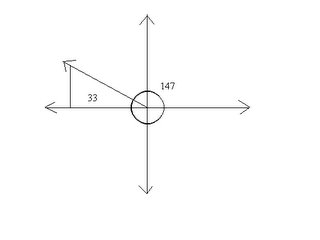 Then find cos147 and cosx(ref). Explain the relationship between the two cosine values. x = 180 - 147 = 33 degrees equals the reference angle measure. Cos33 = 0.838 and cos147 = -0.838. Both of the cosine values are the same, except cos147 is negative. This is because u/r is a negative value (the x value in the 2nd quadrant) over a positive value (r which is always positive).
Then find cos147 and cosx(ref). Explain the relationship between the two cosine values. x = 180 - 147 = 33 degrees equals the reference angle measure. Cos33 = 0.838 and cos147 = -0.838. Both of the cosine values are the same, except cos147 is negative. This is because u/r is a negative value (the x value in the 2nd quadrant) over a positive value (r which is always positive).For additional help go to: http://home.alltel.net/okrebs/page72.html
Amanda!!!!!!!! it's your turn next!!!!!!!!
If you wanna see something totally awesome go to http://www.youtube.com/
then in the search box type "i'm glad I hitched my apple wagon to your star". This music video is by CLAIRE!
If that doesn't work, here's a "magic eye" illusion: