Prep Precalculus D 2006-07: Section 1-6: Reflections, Absolute Values, and Other Transformations

Section 1-6: Reflections, Absolute Values, and Other Transformations

Yay! Section 6!

Main Concepts:

Reflections Across the Coordinate Axes:
- g(x)=-f(x) is a vertical reflection of function across the x-axis.
- g(x)=f(-x) is a horizontal reflection of across the y-axis.

Absolute Value Transformations:
The transformation g(x) = f(x) (The absolute value bars should be around f(x) but no matter what I do, they will not save on the blog).
- Reflects f across the x-axis if f(x) is negative. (negative values become positive) No y-values will be below the x-axis.
- Leaves f unchanged if f(x) is nonnegative. (positive values stay the same)
The transformation g(x) =f(x) (The absolute value bars should be around the x of f(x) but they will not save on the blog, p.s. please tell me how to do it if you figure it out).
- Leaves f unchanged for nonnegative values of x.
- Reflects the part of the graph for positive values of x to the corresponding negative values of x.
- Eliminates the part of f for negative values of x.

An example of this:

If you have the equation y=x^3-2 and you have y(2), you would get y(2) = 2^3 -2 which equals 6. If you had y(-2), would would get y(-2) = -2^3 -2 which equals -10.

Now if you made the equation y = x(with absolute value bars around it)^3 -2, for y(2), you would still get 6. For y(-2), things would be different. The absolute value of -2 is 2, so 2^3 is 8 and 8-2 equals 6. This exemplifies the fact that it does not matter if you put in 2 or -2, you will get the same y value if it is positive or negative.

Even and Odd Functions:
Even Functions:
- f(x)=f(-x)
- Symmetric on y-axis
Odd Function:
- f(x)=-f(-x)
- When a graph is rotated 180 degrees, you end up with the same picture. - Symmetric around the origin.

Example Problem:

Reflection across the x-axis:

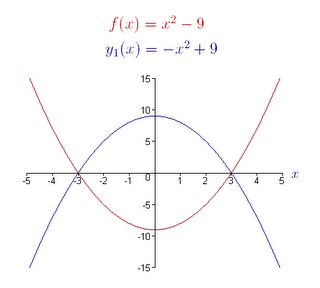
f (x) = x^2 - 9 is our original equation. We will write an equation for the reflection of this pre-image function across the x-axis.

g(x) = - f (x) will give a vertical reflection across the x-axis, so
y1(x) = -f (x)

y1(x) = -f (x) = -(x^2-9) = -x^2 + 9